Vol. 20 - Num. 79
Lectura crítica en pequeñas dosis
Aspectos metodológicos del metaanálisis (1)
aServicio de Gastroenterología. Hospital Infantil Universitario La Paz. Madrid. España.
Correspondencia: M Molina. Correo electrónico: mma1961@gmail.com
Cómo citar este artículo: Molina Arias M. Aspectos metodológicos del metaanálisis (1). Rev Pediatr Aten Primaria. 2018;20:297-302.
Publicado en Internet: 12-09-2018 - Número de visitas: 19102
Resumen
El metaanálisis es un resumen de síntesis cuantitativa habitualmente empleado para analizar los resultados de los estudios primarios de una revisión sistemática. Para que sus conclusiones tengan validez, debe aplicarse la metodología de elaboración de forma correcta, prestando especial atención a la realización de la revisión, combinando los estudios de forma adecuada y representando los resultados de forma correcta. Revisaremos de forma detallada los aspectos relacionados con el estudio de heterogeneidad de los estudios primarios y con la detección del sesgo de publicación, aspectos fundamentales para la validez interna del metaanálisis.
Palabras clave
● Metaanálisis ● Revisión ● Sesgo de publicaciónINTRODUCCIÓN
Vimos en una publicación anterior en esta revista cuál es el desarrollo de la revisión sistemática1, surgido para responder a preguntas concretas sobre un tema en particular utilizando para ello la mejor información existente sobre el tema.
Así, la elaboración de la revisión se estructura en cinco pasos: 1) definición del problema que se quiere resolver mediante la formulación de una pregunta clínicamente estructurada2; 2) búsqueda explícita y global de la información disponible; 3) comprobación de la calidad metodológica de los estudios encontrados; 4) extracción de los datos de interés, y 5) análisis de los datos para llegar a una síntesis de la información que permita sacar las conclusiones para tratar de responder a la pregunta inicial.
Esta síntesis de la información puede ser cualitativa o, siempre que sea posible, cuantitativa, combinando los resultados de los estudios con una metodología estadística definida, lo que constituye el metaanálisis3.
La combinación de los resultados en un metaanálisis permite aumentar la potencia del estudio y obtener conclusiones de estudios contradictorios o con potencia insuficiente. Además, al provenir de poblaciones diferentes (de los diferentes estudios primarios) la aplicabilidad de los resultados es mayor.
Pero para poder aprovechar estas ventajas del metaanálisis se debe ser muy cuidadoso en su elaboración, prestando atención a los procesos clave de su metodología4. En primer lugar, el investigador necesita toda la información disponible, pero puede no obtenerla por defectos en la búsqueda (sesgo de recuperación) o porque solo se publiquen determinados resultados y otros no (sesgo de publicación). En segundo lugar, debe valorarse si los estudios primarios son lo suficientemente homogéneos como para poder “mezclarse” en un análisis de síntesis. En tercer lugar, esta combinación de resultados debe hacerse siguiendo unos métodos matemáticos bien definidos. Por último, deben mostrarse los resultados de la síntesis de forma adecuada, habitualmente mediante una representación gráfica conocida como diagrama de efectos o forest plot.
A lo largo de este artículo y del siguiente se detallarán los aspectos relacionados con el sesgo de publicación, con la forma de estudiar la heterogeneidad de los estudios primarios, con los modelos matemáticos más utilizados para combinar los datos y con la interpretación correcta de un diagrama de efectos. Finalmente, se proporcionarán unas breves indicaciones de los aspectos que deben considerarse cuando se valore una revisión sistemática con metaanálisis.
ESTUDIO DE LA HETEROGENEIDAD DE LOS ESTUDIOS PRIMARIOS
Puede entenderse la heterogeneidad de los estudios primarios como la variabilidad que existe entre los estimadores que se han obtenido en cada uno de esos estudios. Siempre habrá diferencias entre los estudios, aunque solo sea por error de muestreo. El problema más grave, si se quieren combinar, surge cuando existen diferencias importantes debidas a las características de las poblaciones, intervenciones o resultados de los estudios primarios5.
Esto será lo primero que debe hacerse, investigar posibles causas de heterogeneidad, como pueden ser diferencias en los tratamientos, variabilidad de las poblaciones de los diferentes estudios y diferencias en los diseños de los ensayos. Si existe mucha heterogeneidad desde el punto de vista clínico, quizás lo más idóneo sea no hacer metaanálisis y limitarse a un análisis de síntesis cualitativa de los resultados de la revisión.
Si se considera que los estudios se parecen lo suficiente como para intentar combinarlos, se tratará de medir la heterogeneidad con un dato objetivo, utilizando para ello cualquiera de los métodos estadísticos desarrollados hasta la actualidad6,7.
Quizás el más clásico sea la Q de Cochran, que tiene en cuenta las desviaciones entre los resultados de cada estudio y el resultado global, ponderadas según la contribución de cada estudio al resultado global. La Q sigue una distribución χ2 con k - 1 grados de libertad (k es el número de estudios primarios). Si la probabilidad de obtenerse su valor en esta distribución es menor de 0,05 querrá decir que existe heterogeneidad significativa. La Q es un parámetro conservador, por lo que algunos autores proponen utilizar un valor de significación estadística de p <0,1, con lo que se disminuye la probabilidad de cometer un error de tipo II (decir que no hay heterogeneidad cuando sí la hay).
Otros problemas de la Q es que no cuantifica el grado de heterogeneidad, pierde potencia cuando el número de estudios es pequeño y no permite comparar diferentes metaanálisis entre sí si el número de estudios es diferente. Por estos motivos se ha desarrollado otro estadístico, más utilizado en la actualidad: la I2.
La I2 proporciona una estimación de la variabilidad total entre los estudios respecto a la variabilidad total, lo que, dicho de otro modo, es la proporción de la variabilidad debida a diferencias reales entre los estimadores respecto a la variabilidad debida al azar (dicho de forma aún más sencilla, la proporción de variabilidad no debida al azar). Es menos sensible a la magnitud del efecto y al número de estudios.
Su valor va de 0 a 100%, considerándose habitualmente los límites de 25%, 50% y 75% para delimitar cuándo existe una heterogeneidad baja, moderada y alta, respectivamente. La I2 no depende de las unidades de medida de los efectos ni del número de estudios, por lo que sí permite comparaciones con distintas medidas de efecto y entre diferentes metaanálisis con diferente número de estudios.
Existe un tercer parámetro menos conocido, la H2, que mide el exceso del valor de Q respecto del valor que esperaríamos obtener si no existiese heterogeneidad. Un valor de 1 significa que no hay heterogeneidad y su valor aumenta cuando aumenta la heterogeneidad entre los estudios. Pero su verdadero interés es que permite el cálculo de intervalos de confianza para la I2.
Otras veces los autores realizan un contraste de hipótesis con una hipótesis nula de no heterogeneidad utilizando una χ2 o algún estadístico similar. En estos casos, lo que proporcionan es un valor de significación estadística. Si la p es <0,05 se puede rechazar la hipótesis nula y decir que hay heterogeneidad. En caso contrario no se podrá rechazar la hipótesis nula de no heterogeneidad.
En resumen, siempre que se muestre un indicador de homogeneidad que represente un porcentaje indicará la proporción de variabilidad que no es debida al azar. Por su parte, cuando se dé una p habrá heterogeneidad significativa cuando la p sea menor de 0,05.
Como ya se ha comentado, al partir de contrastes de hipótesis cuya hipótesis nula es que los estudios son homogéneos, una p significativa permite rechazarla y concluir que hay heterogeneidad. Pero no se puede aplicar el razonamiento inverso: si no se puede rechazar quiere decir simplemente eso, que no se puede rechazar que no haya heterogeneidad, pero siempre habrá una probabilidad de cometer un error de tipo II si se asume directamente que los estudios son homogéneos.
Por este motivo se han ideado una serie de métodos gráficos para inspeccionar los estudios y comprobar que no hay datos de heterogeneidad, aunque los parámetros numéricos parezcan descartarla.
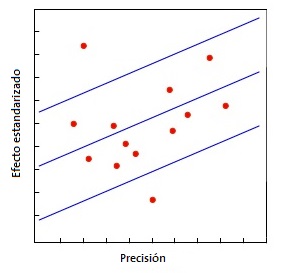
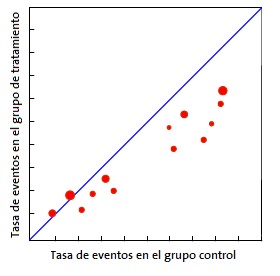
Quizás el más utilizado sea el gráfico de Galbraith8 (Fig. 1), que puede emplearse tanto para ensayos clínicos como para metaanálisis de estudios observacionales. Este gráfico representa la precisión de cada estudio frente a su efecto estandarizado junto con la línea de la ecuación de regresión ajustada y unas bandas de confianza. La posición de cada estudio respecto al eje de la precisión indica el peso de su contribución al resultado global, mientras que su localización fuera de las bandas de confianza indica su contribución a la heterogeneidad. Otra herramienta para metaanálisis de ensayos clínicos es el gráfico de L’Abbé9 (Fig. 2), que representa las tasas de respuesta de los grupos de tratamiento y de control y su posición respecto a la diagonal. Por encima de la diagonal quedan los estudios con resultado favorable al tratamiento, mientras que por debajo están aquellos con resultado favorable al control. Los estudios suelen representarse con un área proporcional a su precisión y su dispersión indica heterogeneidad. Hay que tener en cuenta que este método es aplicable solo a metaanálisis de ensayos clínicos y cuando la variable dependiente es dicotómica.
Si se llega a la conclusión de que existe una heterogeneidad significativa entre los estudios primarios habrá varias posibilidades. La primera, no combinar los estudios primarios y limitarse a la síntesis cualitativa de los resultados. Segunda, hacer un análisis estratificado según la variable que cause la heterogeneidad, siempre que sea posible identificarla. Tercero, la opción más compleja desde el punto de vista estadístico es recurrir a la metarregresión10. Esta técnica es una colección de técnicas de regresión, la más frecuente la regresión lineal múltiple, en el que la variable dependiente es la magnitud del efecto que se valora y las independientes una o varias variables del estudio.
SESGO DE PUBLICACIÓN
Existen una serie de factores que pueden contribuir a este sesgo de publicación11. En primer lugar, es más probable que se publiquen los estudios con resultados significativos y, dentro de estos, es más probable que se publiquen cuando el efecto es mayor. En segundo lugar, los estudios publicados tienen más probabilidad de ser recuperados en la búsqueda que los que no se publican en revistas científicas. Es el caso de tesis doctorales, comunicaciones a congresos, informes de agencias gubernamentales o, incluso, estudios pendientes de publicar realizados por investigadores del tema que se esté tratando. Por este motivo es tan importante hacer una búsqueda que incluya este tipo de trabajos, que se engloban dentro del término de literatura gris.
Por último, pueden enumerarse una serie de sesgos que influyen en la probabilidad de que un trabajo sea publicado o recuperado por el investigador que realiza la revisión sistemática tales como el sesgo de lenguaje (se limita la búsqueda por idioma), el sesgo de disponibilidad (se incluyen solo los estudios que son fáciles de recuperar por parte del investigador), el sesgo de coste (se incluyen estudios que son gratis o baratos), el sesgo de familiaridad (solo se incluyen los de la disciplina del investigador), el sesgo de duplicación (los que tienen resultados significativos tienen más probabilidad de ser publicados más de una vez) y el sesgo de citación (los estudios con resultado significativo tienen más probabilidad de ser citados por otros autores).
Si se delimitan correctamente los criterios de inclusión y exclusión de los estudios primarios y se realiza una búsqueda global y sin restricciones de la literatura médica se habrá hecho todo lo posible para minimizar el riesgo de sesgo, pero nunca habrá certeza de haberlo evitado. Por eso se han ideado técnicas y herramientas para su detección.
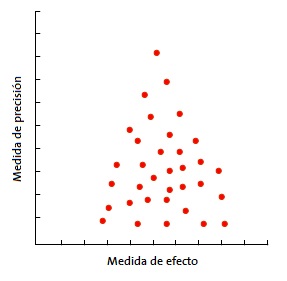
La más usada es el gráfico en embudo o funnel plot (Fig. 3). En él se representa la magnitud del efecto medido (eje X) frente a una medida de precisión (eje Y), que suele ser el tamaño muestral, pero que puede también ser el inverso de la varianza o el error estándar. Se representa cada estudio primario con un punto y se observa la nube de puntos12.
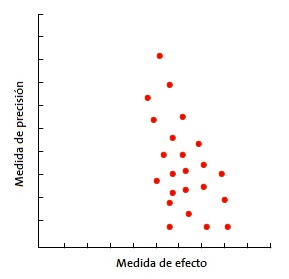
En la forma más habitual, con el tamaño de la muestra en el eje Y, la precisión de los resultados será mayor en los estudios de muestra más grande, con lo que los puntos estarán más juntos en la parte alta del eje y se irán dispersando al acercarse al origen del eje Y. De esta forma, se observa una nube de puntos en forma de embudo, con la parte ancha hacia abajo. Este gráfico debe ser simétrico y, en caso de que no sea así, debe sospecharse siempre un sesgo de publicación. En la Fig. 4 puede verse como “faltan” los estudios que están hacia el lado de falta de efecto: esto puede significar que solo se publican los estudios con resultado positivo.
Este método es muy sencillo de utilizar pero, en ocasiones, pueden existir dudas acerca de la asimetría del embudo, sobre todo si el número de estudios es pequeño. Además, el embudo puede ser asimétrico por defectos de la calidad de los estudios o porque se esté tratando con intervenciones cuyo efecto varíe según el tamaño de la muestra de cada estudio. Para estos casos se han ideado otros métodos más objetivos como la prueba de correlación de rangos de Begg y la prueba de regresión lineal de Egger.
La prueba de Begg estudia la presencia de asociación entre las estimaciones de los efectos y sus varianzas13. Si existe correlación entre ellos, probablemente habrá sesgo de publicación. Esta prueba tiene poca potencia estadística, por lo que es poco fiable cuando el número de estudios primarios es pequeño.
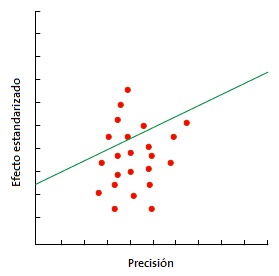
La prueba de Egger (Fig. 5), más específica que la de Begg, consiste en representar gráficamente la recta de regresión entre la precisión de los estudios (variable independiente) y el efecto estandarizado (variable dependiente)14. Esta regresión hay que ponderarla por el inverso de la varianza, lo que aumenta su complejidad estadística. Cuando no hay sesgo de publicación, la recta de regresión se origina en el origen del eje Y. Cuánto más se aleje del cero, mayor evidencia de sesgo de publicación. El valor de p de la regresión que se suele utilizar para sugerir la presencia de sesgo es <0,1 y no <0,05 como se hace habitualmente.
CONFLICTO DE INTERESES
El autor declara no presentar conflictos de intereses en relación con la preparación y publicación de este artículo.
BIBLIOGRAFÍA
- Molina Arias M. La revisión sistemática. Rev Pediatr Aten Primaria. 2013;15:283-5.
- Buñuel JC, Ruiz-Canela J. Cómo elaborar una pregunta clínica. Evid Pediatr. 2005;1:10.
- González de Dios J, Balaguer Santamaría A. Revisión sistemática y metaanálisis (I): conceptos básicos. Evid Pediatr. 2007;3:107.
- Molinero Casares LM. Metaanálisis: claves para interpretar una herramienta de investigación controvertida. Hipertensión. 2001;18:232-40.
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Heterogeneity. Overview. En: Introduction to meta-analysis. John Wiley & Sons; 2009. p. 105-6.
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Heterogeneity. Identifying and quantifying heterogeneity. En: Introduction to meta-analysis. John Wiley & Sons; 2009. p. 107-26.
- Higgins JPT, Thompson SG. Quantifying heterogeneity in a meta-analysis. Stats Med. 2002;21:1539-58.
- Galbraith RF. Graphical display of estimates having differing standard errors. Technometrics. 1998;30:271-81.
- L’Abbé KA, Detsky AS, O’Rourke K. Meta-analysis in clinical research. Ann Intern Med. 1987;107:224-33.
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR.Heterogeneity. Meta-regression. En: Introduction to meta-analysis. John Wiley & Sons; 2009. p. 187-204.
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Publication bias. En: Introduction to meta-analysis. John Wiley & Sons; 2009. p. 77-94.
- Sterne JAC, Egger M. Funnel plots for detecting bias in meta-analysis: guidelines on choice of axis. J Clin Epidemiol. 2001;54:1046-55.
- Begg CB, Mazumdar M. Operating characteristics of a rank correlation test for publication bias. Biometrics. 1994;50:1088-101.
- Egger M, Smith GD, Schneider M, Minder C. Bias in meta-analysis detected by a simple, graphical test. BMJ. 1997;315:629-34.