Vol. 19 - Num. 76
Lectura crítica en pequeñas dosis
¿Qué significa realmente el valor de p?
aServicio de Gastroenterología. Hospital Infantil Universitario La Paz. Madrid. España.
Correspondencia: M Molina. Correo electrónico: mma1961@gmail.com
Cómo citar este artículo: Molina Arias M. ¿Qué significa realmente el valor de p? Rev Pediatr Aten Primaria. 2017;19:377-81.
Publicado en Internet: 30-10-2017 - Número de visitas: 33592
Resumen
El valor de p es un término ampliamente utilizado y mal interpretado por muchos de los lectores de artículos científicos. Se define el significado del valor de p, así como su relación con la fiabilidad del estudio y la importancia clínica de los resultados del mismo.
Palabras clave
● Modelos estadísticosNo cabe duda que muchos de nosotros nos acercamos con aprensión al apartado de métodos de los artículos científicos de la literatura médica, a los cuales nos enfrentamos casi a diario. En lo que respecta a la estadística empleada, aunque los métodos nos resulten familiares, pocas veces entendemos su fundamento. Estamos habituados a leer términos como t de Student, ANOVA, χ2 o U de Mann-Withney, cuya significación exacta se nos escapa y que, sin embargo, son esenciales para saber si el trabajo que estamos leyendo es de alguna utilidad. ¿Y cómo salimos del aprieto? Muy fácil, recurriendo a algo que todos estos métodos tienen en común y que sí creemos que comprendemos bien: todos proporcionan un valor de p que, si es significativo (habitualmente menor de 0,05), nos indica que sí existe el efecto que estamos estudiando.
Así, el valor de p es uno de los datos más apreciados en la lectura científica. ¿Quién no se ha perdido leyendo un artículo especialmente complejo para respirar aliviado al descubrir que la p es significativa? El problema es que, aunque creamos que entendemos su significado, es frecuente que el valor de p sea malinterpretado, de forma que la mayoría albergamos ideas de lo que es la p distintas a lo que realmente es.
Entonces, ¿qué significa realmente el valor de p? Para poder explicarlo, hagamos primero algunas disquisiciones.
Siempre que queramos saber algo sobre una variable biológica (la diferencia de presión arterial según sexo, el efecto de un fármaco, etc.) nos encontraremos con dos problemas de difícil solución. El primero, que a nosotros nos interesa saber el valor de esa variable en la población, pero la población es inaccesible en su totalidad, motivo por el que tenemos que seleccionar una muestra representativa de esa población y trabajar sobre ella. Por ejemplo, si quisiéramos saber si la presión arterial es diferente en hombres y mujeres y pudiésemos medir la presión en toda nuestra población, la diferencia que obtendríamos sería el dato definitivo, sin necesidad de cálculos estadísticos adicionales.
Como esto es imposible, seleccionamos una muestra de hombres y mujeres y comparamos. Y aquí viene nuestro segundo problema, que nos encontramos con el azar. La población de hombres estará centrada alrededor de un valor medio de presión arterial que, si la muestra es representativa, estará próximo al valor medio poblacional al que no podemos acceder. Sin embargo, puede ocurrir que, por azar, la muestra se centre alrededor de otro valor. Lógicamente, será más probable que el valor de la media sea próximo al de la población (repito, siempre que la muestra sea representativa), y será cada vez menos probable que se centre en valores cada vez más extremos o separados. Por este motivo, no podemos nunca estar seguros de que la conclusión que se extraiga con las muestras se cumpla en la población a la que no podemos acceder en su globalidad.
Es imposible librarnos del azar. Su efecto siempre estará presente en nuestros estudios. La buena noticia es que podemos intentar reducirlo (aumentando el tamaño de la muestra, seleccionando con cuidado los participantes, etc.) y, sobre todo, podemos medir cuál es su efecto. Para esto se han diseñado los contrastes de hipótesis.
Volvamos a nuestro ejemplo de la presión arterial. Seleccionamos una muestra de hombres y mujeres, medimos la presión y calculamos el valor medio. Lo más probable es que las dos medias sean diferentes, incluso en el caso hipotético de que en la población la media de presión fuese igual en los dos sexos. Pues bien, esa será nuestra suposición de partida, la llamada hipótesis nula (H0) que, por convenio, consideramos cierta mientras no se demuestre lo contrario1. Frente a esta H0 de no diferencia, definimos una hipótesis alternativa, que dice que el valor es distinto según el sexo. Habitualmente planteamos la H0 como lo contrario de lo que queremos demostrar, de tal manera que, si podemos rechazarla, nos quedemos con la hipótesis alternativa.
Una vez que hemos decidido que no hay diferencias en la población, vamos a calcular cuál es la probabilidad de obtener, por azar, un valor tan diferente o más que el que hayamos obtenido. Aquí es donde entran en juego los diferentes test estadísticos. Para ello, a partir de los resultados, calculamos un estadístico que siga una distribución de probabilidad conocida como, por ejemplo, una t de Student. Esto nos permite saber cuál es la probabilidad de obtener un valor como el obtenido o más alejado de la nulidad, simplemente por azar. Si la probabilidad es alta, diremos que la diferencia se debe al azar y que no es probable que se cumpla en la población. Pero si la probabilidad de obtener este valor por azar es muy baja, podremos decir que, probablemente, sí existe una diferencia real. Dicho de otro modo, rechazaremos la hipótesis nula y abrazaremos la alternativa.
Y este es el valor de p: la probabilidad de obtener, por azar, una diferencia tan grande o mayor de la observada, cumpliéndose que no haya diferencia real en la población de la que proceden las muestras. Así, por convenio suele establecerse que si este valor de probabilidad es menor del 5% (0,05) es lo suficientemente improbable que se deba al azar como para rechazar con una seguridad razonable la H0 y afirmar que la diferencia es real. Si es mayor del 5%, no tendremos la confianza necesaria como para poder negar que la diferencia observada sea obra del azar. Este es el significado de la ansiada p < 0,05 que muchas veces buscamos con determinación al leer los trabajos de las revistas científicas (por no hablar del empeño de los que hacen o financian el trabajo).
Como se puede ver, el valor de p es algo conceptualmente sencillo: una simple medida de la probabilidad de que la diferencia de resultado se deba al azar. Sin embargo, existe mucha confusión en cuanto a su significado. Podemos enumerar una serie de errores habituales sobre lo que no representa el valor de p (Tabla 1)2:
- El valor de p no representa la probabilidad de que la hipótesis nula sea cierta: como hemos dicho, partimos del supuesto de que la hipótesis nula es cierta y es bajo ese supuesto en el que calculamos el valor de p.
- Una p < 0,05 significa que la hipótesis nula es falsa y una p > 0,05 que la hipótesis nula es verdadera: siempre nos movemos en el terreno de la probabilidad. Una p < 0,05 quiere simplemente decir que es poco probable que la H0 sea cierta, luego la rechazamos para abrazar la alternativa, pero siempre tenemos cierta probabilidad de cometer lo que se denomina un error de tipo 1: rechazar la hipótesis nula cuando en realidad es verdadera3. Por otra parte, el valor de p > 0,05 no afirma que la H0 sea verdadera, ya que puede ocurrir que la diferencia sea real y el estudio no tenga potencia para detectarla. Estaremos ante el error de tipo 2: no rechazar la hipótesis de nulidad (y afirmar que no existe el efecto) cuando en realidad sí que existe en la población (pensad, por ejemplo, que el tamaño muestra no sea el suficiente)3. Así como podemos rechazar H0, nunca podemos afirmar lo contrario: H0 solo es falsable, nunca podemos afirmar que sea cierta.
- El valor de p tiene relación con la fiabilidad del estudio, cuyo resultado será más fiable cuanto menor sea la p: en realidad, el valor de p nos indicaría la probabilidad de obtener un valor semejante si se realiza el experimento en las mismas condiciones, pero hay muchos factores que pueden intervenir además del hecho de que exista o no diferencia real: el tamaño de la muestra, la varianza de la variable medida, el tamaño del efecto, la distribución de probabilidad empleada, etc.
- El valor de p nos indica la importancia del resultado. Repetimos, p solo indica la probabilidad de que la diferencia observada se deba al azar. La importancia desde el punto de vista clínico la establece el investigador. Puede haber resultados con un valor de p estadísticamente significativa que carezcan de relevancia clínica y viceversa, valores de p no significativos que pueden tener importancia desde el punto de vista clínico.
| Tabla 1. Errores frecuentes sobre el concepto del valor de p |
|---|
| El valor de p significa la probabilidad de que la hipótesis nula sea cierta |
| Un valor de p < 0,05 significa que la hipótesis nula es falsa |
| Un valor de p > 0,05 significa que la hipótesis nula es cierta |
| Cuánto más pequeño es el valor de p, más fiable es el resultado del estudio |
| Un valor de p < 0,05 indica que el resultado es clínicamente importante |
| Un valor de p > 0,05 indica que el resultado no tiene importancia clínica |

De todo lo dicho hasta ahora, parece claro que cuando planificamos un estudio desearemos que nuestra p nos salga significativa para poder rechazar la hipótesis nula y quedarnos con la hipótesis alternativa, que seguramente afirmará lo que queramos demostrar. Pero ¿qué pasa si la p no sale significativa? ¿Podremos sacar conclusiones del estudio? Pues dependerá de la importancia clínica de los resultados, que habitualmente es establecida por el investigador y sobre la que p tiene poco que decir.
En este punto tendremos que recurrir, además, al uso de intervalos de confianza, término sobre el que también existe bastante confusión4,5. Para decirlo simplemente, un intervalo de confianza del 95% marca los límites entre los que estaría el valor obtenido en el experimento en 95 ocasiones de cada 100 que lo repitiésemos (aunque se parece, no es lo mismo que decir que es el intervalo entre el que está el valor poblacional con un 95% de probabilidad). El intervalo de confianza (IC) nos marca la precisión del estudio y, además, siempre que no incluya el valor nulo para el efecto que estemos midiendo (cero para diferencias de medias, uno para riesgos relativos y odds ratios) querrá decir que el valor de p es significativo. De esta forma, si nos dan el IC podemos ahorrarnos el valor de p.
Pues bien, utilizando el concepto de diferencia clínicamente importante y el IC podremos sacar conclusiones de estudios con p no significativa y, al revés, veremos que hay estudios con p muy pequeñas que tienen muy poca utilidad. Veamos un ejemplo.
Supongamos que queremos valorar el efecto de un fármaco para mejorar la saturación de oxígeno en determinada cardiopatía. Supongamos también que nos interesa un fármaco que mejore la saturación, al menos, en un 5%. Valores menores de este 5% no se considerarán importantes desde el punto de vista clínico. Así, comparamos los valores de saturación en el grupo de intervención y en el control (placebo o el fármaco de referencia) y calculamos los IC de las diferencias entre los dos grupos en cuatro ensayos supuestos cuyos resultados podéis ver en la Fig. 1.
| Figura 1. Intervalos de confianza de los resultados de cuatro estudiosficticios (A, B, C y D) sobre la mejora de la saturación arterial de oxígeno |
|---|
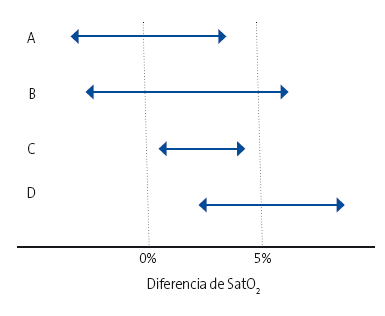 |

No nos dan el valor de las p, pero tampoco los necesitamos para nada. Sabemos que el valor nulo para un intervalo de diferencias de medias es el cero, luego todos los estudios cuyo intervalo cruce el 0% tendrán una p > 0,05 (no significativos) y todos los que estén por encima o por debajo del 0% serán significativos (p < 0,05, siempre que sea este el valor de p elegido por convenio para marcar el límite de significación). Sin embargo, vamos a considerar los estudios de uno en uno.
El estudio A no tiene significación estadística (el intervalo de confianza incluye el valor nulo) y, además, clínicamente no parece importante porque el límite del IC no cruza el valor clínicamente importante del 5%.
El estudio B tampoco es estadísticamente significativo, pero clínicamente podría ser importante, ya que el límite superior del intervalo cae en la zona de relevancia clínica. Si aumentásemos la precisión del estudio (por ejemplo, aumentando la muestra), ¿quién nos asegura que el intervalo no se podría estrechar y quedar por encima del nivel nulo, alcanzando significación estadística? En este caso, la duda no parece muy trascendente porque la variable que estamos midiendo como ejemplo no es muy relevante, pero pensad cómo cambiaría esto si estuviésemos considerando una variable más dura, como la mortalidad.
Por último, los estudios C y D alcanzan significación estadística, pero solo los resultados del D son clínicamente importantes. El estudio C mostraría una diferencia, pero su impacto clínico y, por tanto, su interés, son mínimos, por mucho que el valor de p sea menor de 0,05.
Hasta aquí hemos descrito cuál es el significado exacto del valor de p y su relación con la probabilidad de que las diferencias de efecto de nuestros estudios sean debidas al azar. Este valor no está siempre relacionado con la importancia de los resultados del estudio, de forma que el hallazgo de una p significativa no nos garantiza que la conclusión del trabajo tenga relevancia clínica. Por todo ello, podemos concluir que es aconsejable favorecer el uso de los intervalos de confianza y definir con claridad cuál es la diferencia clínicamente importante.
CONFLICTO DE INTERESES
El autor declara no presentar conflictos de intereses en relación con la preparación y publicación de este artículo.
ABREVIATURAS
H0: hipótesis nula • IC: intervalo de confianza.
BIBLIOGRAFÍA
- Sterne JAC, Smith GD. Sifting the evidence – what’s wrong with significance tests? BMJ. 2001;322:226-31.
- Mark DB, Lee KL, Harrell Jr FE. Understanding the role of p values and hypothesis tests in clinical research. JAMA Cardiol. 2016;1:1048-54.
- Akobeng AK. Understanding type I and type II errors, statistical power and sample size. Acta Paediatr. 2016;105:605-9.
- Carlin JB, Doyle LW. Basic concepts of statistical reasoning: standar errors and confidence intervals. J Pediatr Child Health. 2000;36:502-5.
- McCormack J, Vandermeer B, Allan GM. How confidence intervals become confusion intervals. BMC Med Res Methodol. 2013;13:134.





