La odds ratio puede ser engañosa

Habitualmente hay varias formas de contar una misma verdad sin tener que mentir. Algo parecido pasa también con los trabajos científicos, en los que, en ocasiones, el parámetro elegido para presentar los resultados puede ayudar a disimular una verdad incómoda para el propósito del investigador o, por el contrario, hacer que un efecto modesto parezca mucho más importante.

Ya vimos el caso del uso de medidas de efecto relativas en lugar de absolutas, como puede ser favorecer el uso de la reducción relativa del riesgo, siempre más aparente que la reducción absoluta¹. Otro ejemplo, del que vamos a tratar hoy, es el uso de la odds ratio (OR) en lugar de los riesgos relativos (RR) para tratar de hacer que la asociación entre efecto y exposición parezca más fuerte.

Aunque su significado puede confundirse a veces, odds y riesgo son dos conceptos diferentes. Veámoslo.

El riesgo representa la probabilidad de ocurrir de un evento. Es una proporción entre los sujetos que presentan un evento divido entre el total de sujetos susceptibles de presentarlo. En la típica tabla de contingencia de la Fig. 1 podemos ver cómo calcular los riesgos. El riesgo en los expuestos (Re) se calcula dividiendo el número de enfermos que han estado expuestos entre el total de sujetos expuestos. De manera similar, el riesgo en no expuestos (Ro) se obtiene dividiendo los enfermos que no han estado expuestos entre el total de sujetos sin exposición. Si vamos un paso más allá, podemos calcular el cociente de riesgos entre expuestos y no expuestos, obteniendo la denominada razón de riesgos o RR.

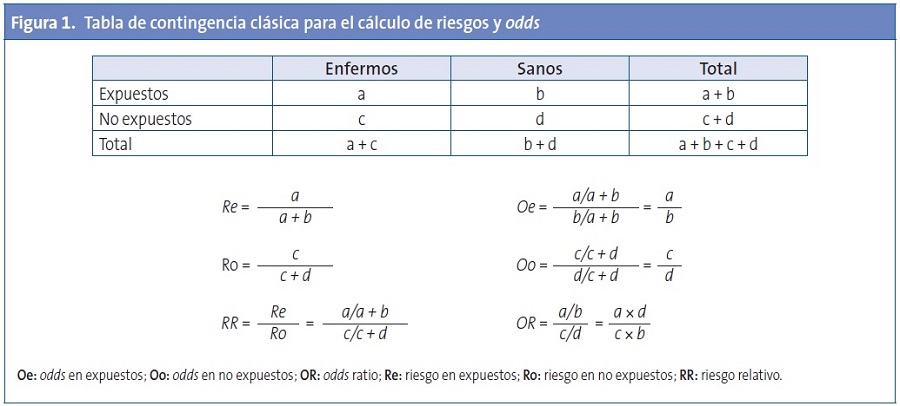
Por otra parte, el concepto de odds es un poco diferente. La odds nos indica cuánto más probable es que se produzca un suceso a que no se produzca [p/(1-p)]. En la Fig. 1 podemos ver cómo se calcula. La odds de enfermar en los expuestos se calcularía dividiendo la probabilidad de enfermar en los expuestos entre la probabilidad de no enfermar en los expuestos. De forma similar, la odds de enfermar en los no expuestos se obtendría dividiendo la probabilidad de enfermar en los no expuestos entre la probabilidad de estar sano en no expuestos. Una vez más, podemos calcular el cociente de las dos odds para obtener la OR, también llamada razón de ventajas. De forma sencilla, podemos calcular la OR como el cociente del producto cruzado de los cuatro elementos de la tabla de contingencia.

Aunque pueden parecer similares, el RR y la OR son conceptos diferentes. Sin embargo, la interpretación es similar en los dos. En ambos casos el valor nulo es uno, lo que significa que el riesgo es igual en expuestos y no expuestos. Un valor mayor que uno indica que la exposición es un factor de riesgo, y un valor menor que uno, que el riesgo es menor en los expuestos. Así, un RR de 2,5 querría decir que los expuestos tienen una probabilidad un 150% mayor de presentar el evento que estemos midiendo. Una OR de 2,5 quiere decir que es una vez y media más probable que ocurra a que no ocurra el suceso en el grupo de expuestos.

Por otra parte, un RR de 0,4 indica una reducción de la probabilidad de ocurrir del 60% en el grupo sometido a la exposición. La OR de 0,4 es más compleja de interpretar, pero viene a decir más o menos lo mismo.

¿Cuándo se usa el RR y cuándo la OR? Depende en gran medida del tipo de diseño que nos ocupe. Para poder calcular el RR tenemos que calcular previamente los riesgos en los dos grupos, y para eso tenemos que conocer la prevalencia o la incidencia acumulada de la enfermedad, por lo que esta medida suele utilizarse en los estudios de cohortes² y en los ensayos clínicos. Podemos ver un ejemplo en la Fig. 2, en la que se muestran los resultados de un estudio de cohortes imaginario sobre afectación coronaria y exposición al tabaco. Como vemos, el RR es 1,2, lo que quiere decir que la enfermedad es un 20% más frecuente en los expuestos al tabaco.

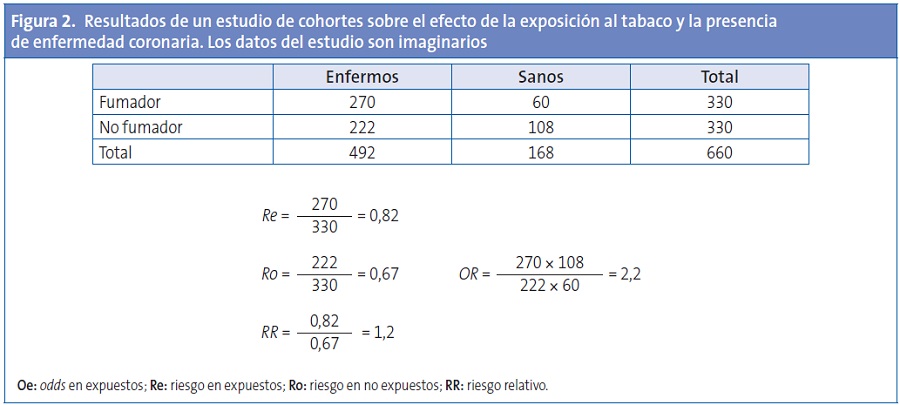
En los estudios en los que no se conoce la prevalencia de la enfermedad, como es el caso de los estudios de casos y controles³, no hay más remedio que usar OR. Otro ejemplo del uso de OR es cuando se recurre a modelos de regresión logística para ajustar por los diferentes factores de confusión detectados, que proporcionan OR ajustadas⁴. De todas formas, el uso de la OR no se limita a los estudios de casos y controles, ya que podemos calcularla también en estudios de cohortes (en lugar del RR). En el ejemplo de la Fig. 2 vemos que la OR es de 2,18. Al igual que el RR, se observa una asociación positiva entre la exposición y la enfermedad, pero nos llama la atención que el valor de la OR es casi el doble que el del RR.

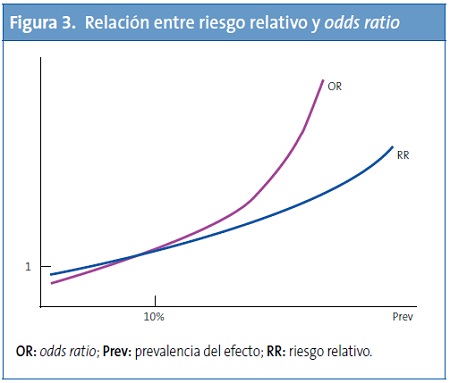
Y esto es así porque el RR y la OR se comportan de forma diferente en función de la prevalencia del efecto que estemos observando. El valor de la OR y el RR es muy similar cuando la prevalencia del efecto es baja, de alrededor del 10%, aunque la OR siempre es un poco más baja que el RR para valores menores de uno y un poco más alta para valores mayores. En la Fig. 3 aparece representada, aproximadamente, la relación entre OR y RR. Como puede verse, a medida que la frecuencia del evento aumenta, la OR crece mucho más rápido que el RR. Y aquí es donde viene la trampa, ya que para un mismo riesgo, el impacto puede parecer mucho mayor si usamos una OR que si usamos un RR. La OR puede ser engañosa cuando el evento es frecuente. Veámoslo con un ejemplo.

Supongamos que hacemos un estudio en salas de cine para comprobar el efecto de la información del público sobre los efectos nocivos para la salud de beber en exceso bebidas edulcoradas. En unas salas ponemos carteles explicando los efectos nocivos y en otras no ponemos nada, y registramos el número de espectadores que compran un refresco para tomarlo mientras ven la película. Los resultados aparecen reflejados en la Fig. 4, en la que consideramos como exposición la ausencia de información.

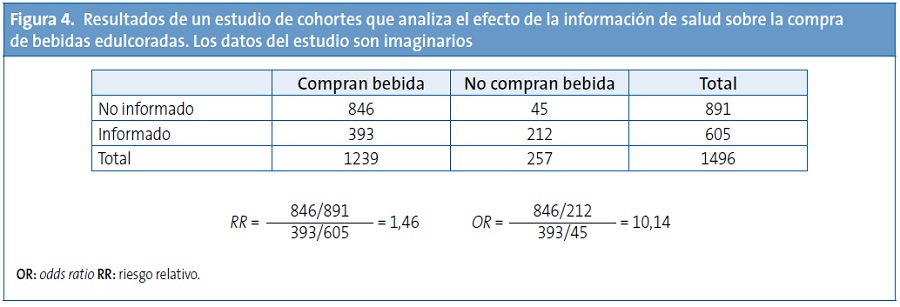
El Re (riesgo de comprar la bebida si no hay carteles) es de 0,95. Por otra parte, el Ro (cuando ponemos carteles) es de 0,65. Vemos que hay una reducción absoluta del riesgo de 0,3, lo que quiere decir que tenemos que mostrar un cartel a 3-4 personas para que una deje de comprar la bebida. ¿Os parece que el impacto de la intervención es importante? Yo diría que es más bien modesto, aunque es mejor que no hacer nada. Veamos qué pasa con el RR. Su valor es de 1,46, un valor modesto para un estudio observacional. Sin embargo, si calculamos la OR vemos que es de 10,14, casi diez veces superior al RR. Esto se explica por la alta prevalencia del efecto (la gran mayoría compra la bebida).

El problema viene a la hora de presentar los resultados. Si queremos ser más fieles a la realidad debemos emplear una medida absoluta como la reducción absoluta del riesgo o el número necesario a tratar (el inverso de la reducción absoluta). Podemos, incluso, presentar el RR, ya que se trata de un estudio de cohortes en el que podemos definir la prevalencia del efecto en los dos grupos. Pero si yo tengo un conflicto de interés (por ejemplo, fabrico los carteles), ¿qué medida creéis que emplearía para presentar los resultados? Sin duda, la OR, mucho más aparente y que parece magnificar mucho más el efecto de la intervención.

Así que, cuando veamos OR en estudios donde la prevalencia del efecto es alta, siempre intentaremos calcular el RR. Si se ha calculado a partir de una tabla de contingencia en un ensayo o un estudio de cohortes, podremos calcularlo con facilidad a partir de los datos del estudio. En el caso de estudios que muestran OR producto de un modelo de regresión logística, la cosa puede ser más complicada, aunque si disponemos de la prevalencia del efecto podemos utilizar la siguiente fórmula para calcular los RR equivalentes.

Esta medida del RR nos informará de manera más real y podremos compararla con las OR proporcionadas por los autores para sacar nuestra propias conclusiones del estudio.

CONFLICTO DE INTERESES

El autor declara no presentar conflictos de intereses en relación con la preparación y publicación de este artículo.

ABREVIATURAS: OR: odds ratio • Re: riesgo en los expuestos • Ro: riesgo en no expuestos • RR: riesgo relativo.

BIBLIOGRAFÍA

1. Molina M. Cálculo de la reducción del riesgo y el número necesario de pacientes a tratar. Rev Pediatr Aten Primaria. 2012;14:369-72.
2. Molina M, Ochoa C. Estudios observacionales (II). Estudios de cohortes. Evid Pediatr. 2014;10:14.
3. Molina M, Ochoa C. Estudios observacionales (III). Estudios de casos y controles. Evid Pediatr. 2014;10:33.
4. Schiattino A, Rodríguez M, Pasarín MI, Regidor E, Borrell C, Fernández E. ¿Odds ratio o razón de proporciones? Su utilización en estudios transversales. Gac Sanit. 2003;17:70-4.

Comentarios

Este artículo aún no tiene comentarios.