Las trampas de la estadística

INTRODUCCIÓN

Como ya comentamos en una publicación anterior, la mayor parte de los trabajos científicos que se publican en la actualidad están aquejados de graves defectos en su metodología¹, en ocasiones debidos a la falta de formación de los autores y revisores, pero también, en otras ocasiones, debidos a la intencionalidad de transmitir algún mensaje concreto a través de los resultados del trabajo.

Muchos de estos errores pueden ser relativamente fáciles de detectar si hacemos una lectura crítica del trabajo, para lo cual dimos una serie de pistas útiles que nos permitiesen evitar malgastar nuestro limitado tiempo con la lectura de trabajos de escasa validez².

Quizás el aspecto más difícil de valorar para el clínico sin formación en metodología sean los aspectos relacionados con los estudios estadísticos utilizados para el análisis de los datos del trabajo. Es aquí, sin duda, donde nos pueden engañar con más facilidad utilizando, o dejando de utilizar, los métodos de análisis adecuados en favor de otros que proporcionen unos resultados más vistosos o apetecibles.

Daremos a continuación una serie de pistas que, sin ser expertos en estadística, nos permitan detectar algunas de estas posibles trampas.

1. ¿SE HA UTILIZADO ALGÚN MÉTODO ESTADÍSTICO?

Esta pregunta puede parecer obvia, pero no lo es en absoluto. Aunque afortunadamente con poca frecuencia, en alguna ocasión podemos encontrarnos con un trabajo cuyos autores se limitan a comparar los resultados para extraer directamente sus conclusiones sin hacer uso de metodología estadística alguna. Evidentemente, toda comparación deberá hacerse con el adecuado contraste de hipótesis, e indicarse su nivel de significación y la prueba estadística utilizada. En caso contrario las conclusiones no serán válidas.

2. LA COMPARABILIDAD BASAL DE LOS GRUPOS DE ESTUDIO

Todo estudio, especialmente si se trata de un ensayo clínico, debe incluir una tabla que muestre las características basales de los grupos de control e intervención. Esto es así porque para poder valorar el efecto de la intervención se necesita que los grupos sean comparables en todo, excepto en la intervención estudiada.

Aunque cada vez con menos frecuencia, podemos ver en estas tablas las diferencias en los distintos parámetros con su correspondiente valor de p para decidir si se deben o no al azar, pero esto, si lo pensamos un poco, no tiene mucho sentido. Si hemos repartido los participantes entre los dos grupos al azar, cualquier diferencia se deberá al azar, sea cual sea el valor de p. De todas formas, el valor de p tampoco tiene mucho significado en este caso, ya que el tamaño de la muestra del estudio está calculado para valorar la diferencia del efecto de la intervención en los dos grupos y no para valorar las diferencias basales entre ellos. Lo realmente interesante será valorar la importancia clínica de las diferencias que podamos observar.

Podemos tener diferencias relevantes que no alcancen valor significativo desde el punto de vista estadístico por no ser la muestra lo suficientemente grande. Por tanto, será el autor el que debe decidir si las diferencias observadas son relevantes para el estudio y hacer el ajuste pertinente en la fase de análisis de los resultados.

3. EL AZAR NO PRODUCE GRUPOS IGUALES

La aleatorización es una parte fundamental de cualquier ensayo clínico, por lo que debe estar claramente definido cómo se ha hecho. Con relativa frecuencia vemos trabajos en los que el grupo control y el de intervención tienen el mismo número de participantes. Pues bien, esto es altamente improbable si se hace un muestreo aleatorio simple. Por ejemplo, si aleatorizamos 100 individuos, la probabilidad de que el azar reparta exactamente 50 a cada grupo es del 9% (0,09). Esta probabilidad es aún menor cuanto mayor sea el número de participantes, por lo que podremos desconfiar cuando los autores consigan grupos iguales con un muestreo aleatorio.

Esto no tiene nada que ver con otras situaciones en las que el muestreo no es aleatorio simple. Existen técnicas, como el muestreo estratificado, por bloques o las técnicas de minimización, que tratan de asegurar un número similar de participantes en todos los grupos. Estas técnicas son lícitas si se utilizan de forma adecuada y sí nos pueden dar fácilmente grupos con un mismo número de participantes.

4. OPERACIONES CON DATOS CUALITATIVOS

El tipo de datos utilizados y las operaciones que se hagan con ellos es otro aspecto que debemos tener en cuenta. Hay que juzgar con especial atención la aritmética que se haga con variables cualitativas. Si la variable es dicotómica puede codificarse como cero y uno y hallarse la media aritmética, pero el resultado debe interpretarse con precaución.

También es posible hacer operaciones similares con escalas de variables cualitativas, pero para que esto tenga sentido debe haber una graduación constante y proporcional entre los diferentes valores de la variable. De lo contrario, las operaciones aritméticas carecerán de sentido.

Aunque a veces es útil categorizar una variable continua, esta transformación debe tener un sentido clínico lógico o de gradación; sin embargo, esto no siempre es así, por lo que se pueden encontrar diferencias estadísticas significativas donde a priori no las hay.

5. ¿SE HA EMPLEADO LA PRUEBA ESTADÍSTICA CORRECTA?

Este puede ser uno de los puntos más difíciles de valorar para el no experto en estadística. Un error frecuente es utilizar pruebas paramétricas sin comprobar previamente que los datos siguen una distribución normal. Esto es así porque las pruebas no paramétricas suelen ser bastante más conservadoras, por lo que siempre es más fácil obtener significación estadística con una prueba paramétrica.

Además de la asunción de normalidad, la mayor parte de las pruebas de contraste de hipótesis, como la t de Student o el análisis de la varianza, precisan tener en cuenta la independencia de las muestras o la existencia de homocedasticidad (igualdad de varianzas), comprobaciones que se pasan por alto en numerosos trabajos.

Un error frecuente al comparar medias de más de dos poblaciones es realizar comparaciones dos a dos una vez obtenida significación estadística con el análisis de la varianza (que solo nos indica que no todas la medias son iguales, pero no nos dice cuáles son diferentes entre sí). En estos casos es preceptivo realizar siempre alguna corrección, como la de Bonferroni, ya que al aumentar el número de comparaciones aumenta el riesgo de obtener una significativa por azar.

A modo orientativo, en la Tabla 1 se muestran las pruebas correctas para realizar comparaciones de medias según el número de muestras, la presencia de homocedasticidad y la distribución de los datos.

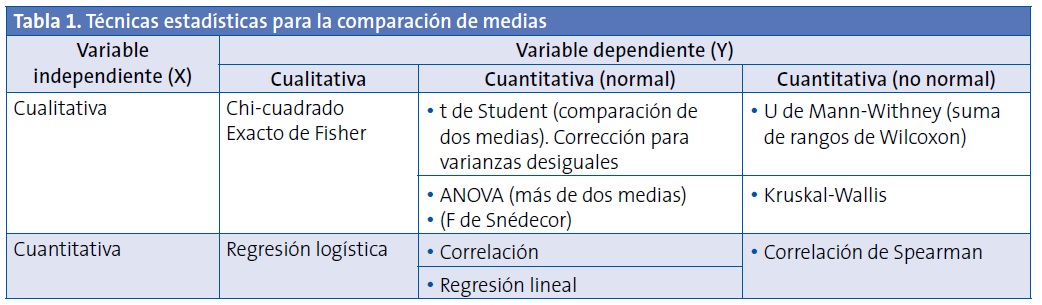
Otro aspecto que debemos tener en cuenta es qué medidas de centralización y dispersión se han utilizado. En casos de distribuciones no normales o muy sesgadas, es preferible utilizar la mediana y los recorridos intercuartílicos en lugar de la media y la desviación típica. Esto puede evitarse utilizando medidas de centralización robustas, como la media recortada o la media geométrica, o bien aplicando a los datos una transformación como la logarítmica, inversa, etc.

Transformar los datos es completamente lícito, siempre que se tenga después la precaución de deshacer la transformación a la hora de interpretar los resultados.

Por último, llamar la atención sobre la existencia de datos pareados. En estos casos, el análisis estadístico debe realizarse empleando las pruebas adecuadas para análisis de datos pareados.

6. ¿POR QUÉ HAN USADO UN MÉTODO TAN RARO?

Eso es lo que nos preguntamos a veces cuando leemos la descripción de una técnica estadística de la que nunca antes habíamos oído hablar. Si los datos del trabajo son datos estándares recogidos de forma estándar, ¿por qué utilizar un método raro?

En estos casos debe exigirse de los autores que justifiquen su elección e, idealmente, que aporten una cita bibliográfica donde se describa la técnica empleada. En estadística hay que elegir la técnica correcta para cada ocasión y no buscar aquella que nos dé el resultado que más nos guste.

7. ¿SE HA RESPETADO EL PROTOCOLO ORIGINAL?

El análisis de los datos debe realizarse siguiendo siempre el protocolo descrito a priori. Debemos desconfiar de los estudios post hoc que no estaban planificados desde el comienzo. Si buscamos lo suficiente entre los grupos de participantes siempre podremos encontrar uno que se comporte de una forma determinada. Hacer grupos de forma retrospectiva puede conducir a errores de interpretación de los resultados.

Otra conducta inaceptable es la finalización del ensayo antes de tiempo por observarse buenos resultados. Siempre que sea posible, el seguimiento debe ser completo para comprobar que los buenos resultados se mantienen hasta el final. Por supuesto, sí es lícito finalizar prematuramente por objetivarse toxicidad o algún efecto adverso grave para los participantes.

8. ¿CON UNA O CON DOS COLAS?

El contraste de hipótesis unilateral (con una cola) es menos exigente que el bilateral a la hora de conseguir significación estadística, por lo que algunos autores presuponen la dirección del efecto de la intervención y realizan un contraste unilateral. Sin embargo, y como norma general, no es bueno asumir la dirección del efecto, por lo que siempre es preferible el contraste bilateral.

9. MANEJO DE VALORES EXTREMOS

Los valores extremos (outliers) son aquellos que se alejan mucho del valor central de la distribución. Pueden deberse a errores de cálculo, de medición o de transcripción de los valores de las variables, pero también pueden ser reales y deberse a la idiosincrasia de la variable que estemos midiendo. Existe cierta tendencia a eliminarlos del análisis, pero esto solo es lícito en el caso de que se deban a algún tipo de error.

Su presencia debe tenerse en cuenta a la hora de analizar los resultados. Existen métodos estadísticos robustos que permiten ajustar las desviaciones producidas por los valores extremos, aunque suelen ser más sofisticados que los habituales. En cualquier caso, debemos desconfiar de la validez de los resultados si existen valores extremos y no se realiza ningún tipo de ajuste.

10. CORRELACIÓN, REGRESIÓN Y LA TRAMPA DE LA CAUSALIDAD

Esta es una fuente bastante común de error. El coeficiente de correlación de Pearson investiga la fuerza de la relación lineal entre dos variables continuas. Solo nos dice si están relacionadas, pero no si son dependientes o independientes, y mucho menos si una es causa de la otra. Tampoco sirve para calcular el valor de una variable a partir de otra. Para eso tenemos que recurrir a la regresión, que mide la naturaleza de la relación entre las dos variables y nos da una idea de la dirección de la influencia de una variable sobre la otra. En cualquier caso, insistimos, ni correlación ni regresión implican causalidad.

Otro error que podemos encontrar es el uso del coeficiente de correlación de Pearson sin que se cumplan las exigencias para su uso: las variables deben seguir una distribución normal, deben ser estructuralmente diferentes (no tiene sentido calcular la correlación entre, por ejemplo, peso e índice de masa corporal, que incluye el peso) y solo debe haber dos medidas por cada participante en el estudio. Lo correcto es, además, acompañarlo de un valor de p o del correspondiente intervalo de confianza.

En los casos en los que no se cumplen las condiciones previas, debe utilizarse el coeficiente de correlación de Spearman, que es el equivalente no paramétrico.

Otro mal uso del coeficiente de correlación es el que se comete con frecuencia al utilizarlo para comparar los resultados entre dos observadores distintos. En estos casos lo correcto es utilizar un coeficiente de correlación intraclase (para variables continuas) o un índice kappa para variables dicotómicas.

Por último, otro error frecuente y similar al anterior es comparar dos métodos de medición mediante una correlación o regresión lineal, por ejemplo comparar la glucemia capilar con la venosa. Esto no es correcto, ya que estas pruebas estudian la relación entre dos variables ya sea de forma simétrica (correlación) o asimétrica (regresión). En estos casos hay que utilizar la regresión de Passing y Bablok, que tiene la ventaja de estimar una recta de regresión no sesgada mediante métodos no parámetricos.

11. EL VALOR DE P Y SUS USOS

El valor de p es la probabilidad de que la diferencia de efecto observada entre dos o más grupos no se deba al azar o, dicho de otro modo, la probabilidad de cometer un error de tipo I (rechazar la hipótesis nula siendo cierta). No debemos olvidar que este valor de significación estadística es totalmente arbitrario, por lo que tiene mucha más utilidad el uso de los intervalos de confianza³, que nos permiten valorar también la importancia clínica de los resultados, incluso aunque las diferencias no alcancen significación estadística.

12. EL USO DE MEDIDAS MÁS PRESENTABLES

Siempre hay muchas formas de presentar los resultados y, aunque todas digan en el fondo lo mismo, la apariencia puede ser muy diferente según el parámetro que escojamos.

Quizás el ejemplo más claro y más frecuente sea el de la utilización de medidas de impacto relativas en lugar de las absolutas. Es frecuente que los autores del trabajo nos muestren la estimación del efecto utilizando la reducción relativa del riesgo en lugar de la reducción absoluta o el número necesario de pacientes a tratar⁴. Esto es así porque el valor de la reducción relativa es mayor que el de la absoluta, por lo que parece que el impacto de la intervención es mayor. Sin embargo, la reducción absoluta y, sobre todo, el número necesario a tratar son las medidas que nos informan del valor absoluto del impacto de nuestra intervención. Dado que las medidas absolutas se calculan fácilmente a partir de los mismos datos que las relativas, deberemos desconfiar cuando no se nos ofrezcan en el trabajo: quizás el efecto no sea tan importante como los autores nos pretenden hacer ver.

Otro ejemplo podemos encontrarlo en los estudios sobre pruebas diagnósticas, en los que con frecuencia solo se muestran indicadores como sensibilidad o especificidad, ocultándose los cocientes de probabilidades, que son los que mejor estiman el rendimiento de la prueba.

Otra trampa que puede observarse de forma ocasional es mostrar los resultados utilizando la media más menos el error estándar en lugar de la media más menos la desviación estándar. La razón para esto es casi pueril: el error estándar es mucho menor que la desviación estándar, con lo que se transmite la impresión de una mayor precisión de los resultados. Sin embargo, los dos términos representan conceptos totalmente distintos. La desviación estándar mide la separación media de los valores de la distribución respecto de la media (por lo que es útil como medida de dispersión), mientras que el error estándar es una estimación de cómo variaría la media de la distribución si la repitiésemos con distintas muestras de la población: nada que ver la una con el otro.

Por último, hacer referencia al maquillaje de los gráficos que puede llevarse a cabo según las unidades de medida que los autores escojan para la representación gráfica. Siempre debemos observar estas unidades y tratar de extraer la información del gráfico más allá de lo que pueda parecer que representan a primera vista.

Y con esto terminamos de exponer algunos de los errores más habituales que podemos encontrar entre los métodos estadísticos utilizados en los trabajos científicos. En la Tabla 2 se resumen algunas de estas posibles trampas que debemos estar preparados para detectar.

CONFLICTO DE INTERESES

El autor declara no presentar conflictos de intereses en relación con la preparación y publicación de este artículo.

BIBLIOGRAFÍA

1. Altman DG. Poor-quality medical research: what can journal do? JAMA. 2002;287:2765-7.
2. Molina Arias M. Razones para dejar de leer un artículo. Rev Pediatr Aten Primaria. 2014;16:87-91.
3. Molina Arias M. El significado de los intervalos de confianza. Rev Pediatr Aten Primaria. 2013;15:91-4.
4. Molina Arias M. Cálculo de la reducción del riesgo y el número necesario de pacientes a tratar. Rev Pediatr Aten Primaria. 2012;14:369-72.

Comentarios

Este artículo aún no tiene comentarios.