El problema de las comparaciones múltiples

Como ya expusimos anteriormente, un ensayo clínico debe estar diseñado para responder con claridad a una pregunta clínica específica¹. En este sentido, lo habitual es que se valore una variable principal de resultado (en ocasiones alguna más) para determinar el efecto de la intervención estudiada frente al grupo placebo o de comparación. De esta forma, el contraste de hipótesis principal del estudio se hace comparando el resultado de esa variable en los dos grupos que se formaron mediante el reparto aleatorio de los participantes en el ensayo.

Sin embargo, cada vez es más frecuente encontrar estudios en los que la comparación de los resultados no se hace entre estos dos grupos, sino entre grupos diversos obtenidos de subdivisiones de la población de estudio que se forman por características basales no aleatorizadas².

Las fuentes de comparación múltiple son diversas. Un caso típico en estudios observacionales sería el estudio de cohortes en el que se valoran varios resultados que pueden ser productos de la misma exposición. Otro caso es el de los múltiples análisis realizados en el trascurso de un ensayo clínico secuencial³, buscando el punto que nos permita dar por terminado el estudio según una regla de finalización previamente especificada.

Pero quizás el más observado en la actualidad es el caso de los llamados estudios post hoc. Cuando los autores del ensayo no obtienen resultados satisfactorios en el sentido de no poder demostrar el efecto de la intervención ensayada, es relativamente frecuente que se lleven a cabo estas maniobras para dividir la población del ensayo en grupos según características no aleatorizadas para tratar de demostrar la existencia de un efecto significativo entre alguno de estos grupos. Es una forma de dar otra vuelta de tuerca a los datos obtenidos, tratando de obtener algún resultado presentable para que el ensayo sirva para algo. Claro que si se hace con esta motivación, los autores se olvidan de dos hechos. El primero, que un resultado no significativo puede ser también útil desde el punto de vista clínico. El segundo, que si torturamos los datos lo suficiente puede que acaben por decirnos lo que nos guste, pero podemos pagar un alto precio por ello. Y este precio no es otro que el de cometer un error de tipo I y dar por bueno un efecto que en realidad no existe⁴.

Recordemos que siempre que hacemos un contraste de hipótesis establecemos una hipótesis nula (H0) que dice que la diferencia observada entre los grupos de intervención y control se debe al azar⁵. A continuación, calculamos la probabilidad de que la diferencia se deba al azar y, si es menor que un valor determinado (habitualmente 0,05), rechazamos la H0 y afirmamos que es altamente improbable que la diferencia se deba al azar, por lo que la consideramos real. Pero claro, altamente improbable no significa seguro. Siempre hay un 5% de probabilidad de que, siendo la H0 cierta, la rechacemos, dando por bueno un efecto que en realidad no existe. Esto es lo que se llama cometer un error de tipo I.

Pues bien, el problema de las comparaciones múltiples es que cuantas más comparaciones realicemos, mayor será la probabilidad de cometer un error de tipo I y obtener un falso positivo (dar por bueno el efecto que en realidad no existe). Pensemos un poco sobre ello.

La probabilidad de un falso positivo con cada contraste de hipótesis es del 5% (0,05) y la de acertar del 95%. Si hacemos cien contrastes, esperamos equivocarnos una media de cinco veces, simplemente por azar. Si hacemos dos contrastes, la probabilidad de equivocarnos será igual a 0,05 × 0,05, ya que son sucesos independientes. Si hacemos n contrastes, la probabilidad será de 0,05 por 0,05 n veces, o 0,05ⁿ.

Así que podemos preguntarnos: si hacemos n comparaciones, ¿cuál es la probabilidad de tener al menos un falso positivo? Esto es un poco laborioso de calcular, porque habría que calcular la probabilidad de 1, 2…, n - 1 y n falsos positivos utilizando probabilidad binomial. Así que recurrimos a un truco muy utilizado en el cálculo de probabilidades, que es calcular la probabilidad del suceso complementario. Me explico. La probabilidad de algún falso positivo más la probabilidad de ninguno será de 1 (100%). Luego la probabilidad de algún falso positivo será igual a uno menos la probabilidad de ninguno.

¿Y cuál es la probabilidad de ninguno? La de no cometer error en cada contraste ya hemos dicho que es de 0,95. La de no cometer errores en n contrastes será de 0,95ⁿ. Así que la probabilidad de tener al menos un falso positivo será de 1 - 0,95ⁿ.

Vamos a aplicar esto que hemos explicado a un ejemplo real de la literatura. Se trata de un ensayo sobre el efecto del esomeprazol para el tratamiento de los síntomas de enfermedad por reflujo en lactantes⁶. En este trabajo, los autores valoran el efecto del tratamiento con esomeprazol frente al placebo en un grupo de lactantes diagnosticados de enfermedad por reflujo, utilizando como variable principal de resultado el tiempo en suspender el tratamiento por falta de respuesta clínica.

Pues bien, los autores no encuentran diferencias entre el grupo de intervención y el de placebo, así que recurren al estudio post hoc para tratar de sacar alguna conclusión aprovechable. Dividen la población del ensayo en 14 grupos diferentes según características que no tienen nada que ver con la aleatorización inicial y obtienen un resultado estadísticamente significativo. Bueno, los autores pueden respirar algo más tranquilos: al menos hay un subgrupo de pacientes en los que parece que la intervención sí es eficaz. Pero ¿realmente pueden estar razonablemente seguros de que el efecto detectado es real y no es debido a la trampa matemática de las comparaciones múltiples?

No tenemos más que aplicar la fórmula que dedujimos antes y calcular cuál es la probabilidad de obtener al menos un falso positivo por azar si hacemos 14 comparaciones: 1 - 0,95¹⁴, que es igual a 0,51. O sea, que si hacemos 14 comparaciones tenemos un 51% de probabilidad de obtener uno o más falsos positivos por simple azar. Pero es que hay más datos que apoyan esta posibilidad.

En la Fig. 1 se representa la distribución de los valores de las p obtenidas en las distintas comparaciones. Podemos ver cómo estas probabilidades se disponen según una distribución uniforme entre el cero y el uno. Cuando esto es así, apoya la posibilidad de que la p significativa sea debida únicamente al azar⁷.

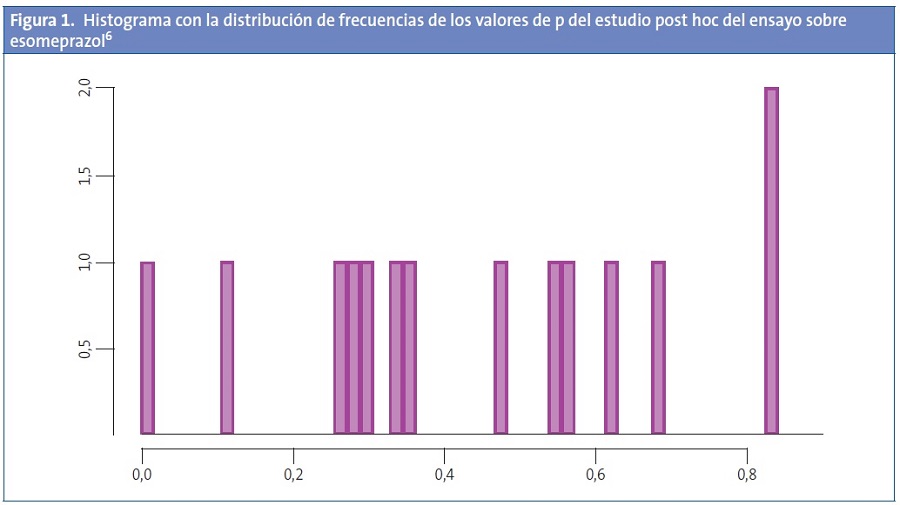
Además, existen una serie de datos que nos pueden hacer sospechar que los valores significativos obtenidos pueden ser debidos, sin más, al azar⁴. Por ejemplo, sospecharemos cuando haya muchas comparaciones y solo unas pocas sean significativas, o cuando los valores de la p con significación sean modestos, entre 0,01 y 0,05. Otra pista nos la puede dar el hecho de que la comparación significativa tenga un patrón o dirección inconsistente con el resto de comparaciones (por ejemplo, todos riesgos relativos mayores que uno excepto el significativo).

La lección de toda esta historia es que el ensayo clínico está diseñado para detectar un efecto en su población global, por lo que el estimador más fiable para el resultado de uno de los subgrupos seguirá siendo el estimador global del ensayo. Por todo lo dicho, deberemos considerar de forma muy crítica los resultados obtenidos de las comparaciones múltiples, especialmente de los análisis exploratorios postaleatorización. Para ello pueden establecerse una serie de recomendaciones².

Primero, todo análisis que se lleve con los resultados debería estar especificado de forma prospectiva en la planificación del estudio. Segundo, se debe evitar construir numerosos subgrupos y limitarse a aquellos con plausibilidad biológica según nuestros conocimientos. Tercero, analizar subgrupos solo si los resultados del grupo global son significativos. Cuarto, tratar de identificar posibles factores de modificación de efecto. Quinto, llevar a cabo alguna técnica de ajuste para comparaciones múltiples, como puede ser la de Bonferroni⁸. Y sexto, quizás lo más importante, evitar sobrevalorar las diferencias que podamos encontrar en los resultados en los distintos subgrupos.

CONFLICTO DE INTERESES

El autor declara no presentar conflictos de intereses en relación con la preparación y publicación de este artículo.

ABREVIATURAS: H0: hipótesis nula.

BIBLIOGRAFÍA

1. Molina Arias M. El ensayo clínico aleatorizado. Rev Pediatr Aten Primaria. 2013;15:393-6.
2. Kaul S, Diamond GA. Trial and error. How to avoid commonly encountered limitations of published clinical trials. J Am Coll Cardiol. 2010;55:415-27.
3. Molina Arias M, Ochoa Sangrador C. Ensayo clínico (I). Definición. Tipos. Estudios cuasiexperimentales. Evid Pediatr. 2014;10:52.
4. Sainani KL. The problem of multiple testing. PM R. 2009;1:1098-103.
5. Molina Arias M. Sota, caballo y rey: el contraste de hipótesis. 2014 [en línea] [consultado el 17/11/2014]. Disponible en http://anestesiar.org/2014/sota-caballo-y-rey-el-contraste-de-hipotesis/
6. Winter H, Gunasekaran T, Tolia V, Gottrand F, Barker PN, Illueca M. Esomeprazole for the treatment of GERD in infants ages 1-11 months. J Pediatr Gastroenterol Nutr. 2012;55:14-20.
7. Glickman ME, Rao SR, Schultz MR. False discovery rate control is a recommended alternative to Bonferroni-type adjustments in health studies. J Clin Epidemiol. 2014;67:850-7.
8. McLaughlin MJ, Sainani KL. Bonferroni, Holm and Hochberg corrections: fun names, serious changes to p values. PM R. 2014;6:544-6.

Comentarios

Este artículo aún no tiene comentarios.